
本課程接下來介紹的是類神經網路 (NN)的運作原理,上面所示的是一個基本的NN,
有一個3個neuron 的隱藏層和一個nueron 的輸出層,
如果我們放大隱藏層來看:

如果我們要解決的是前文提到的判斷衣服是否暢銷的問題,
那我們神經元裡放的activation function 就會是 sigmoid function,
在橘色的input 值被傳送到第一層隱藏層時,會被給予 w 與 b 兩種數字,
w 指的是 weighting (權重), b 指的是 bias (偏差),
如果是熟悉 linear regression 的人應該就能馬上聯想到熟悉的 wx + b 公式,
由於每一個神經元都會有自己的 weighting 與 bias,所以會在右下角加入下綴。
而運算完 wx +b,又會被代入 activation function 裡,
activation function 計算完的數值 (0.3, 0.7, 0.2) 才會是被傳送到輸出層的數值,

這三個數值會再經過output layer 中的acitvation function 計算後,成為最終看到的輸出值,

再透過 decision 來決定要分類成 1 或是0 。
如果是擁有多個隱藏層的類神經網路呢?
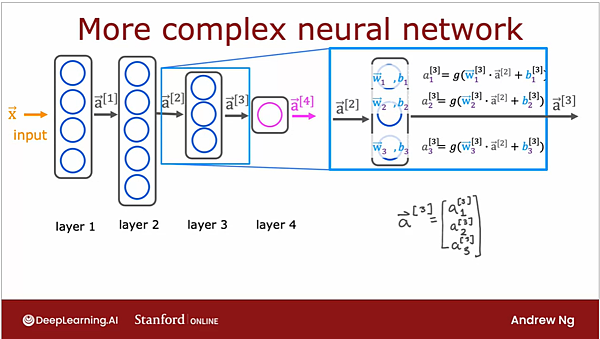

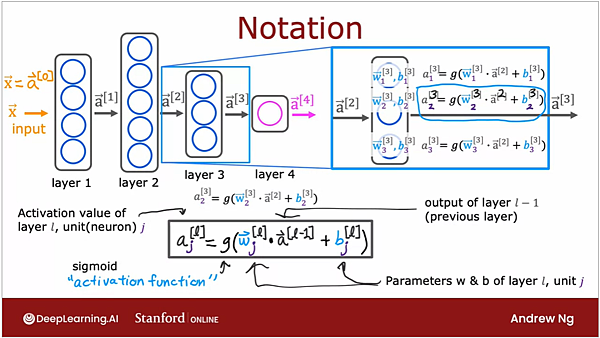
在標示的部分,會把屬於哪一個隱藏層的資訊標示在右上角,
另外要特別注意,前一層的output (前一層 activation function算完的結果) 是沒有右下角的標示的。
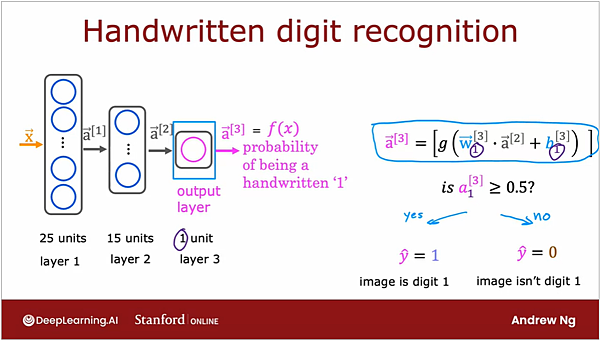
接下來以手寫辨識來說明 multi layer perceptron 的運作:

在做手寫辨識時,同樣是以圖像的方式來處理,黑色 (沒有寫)的地方就給予色碼255,有寫的地方是色碼0,
這些資訊會直接被當成 input,丟進演算法中建立起色碼的組合與標記 (y) 之間的關係,
計算過程跟之前提到的一樣,如果有25個神經元就會有25個 (w,b)組合,各自餵進activation 中形成下一層的輸入值。

在輸出層中只有一個神經元,所以他不會像前幾層一樣是個向量,而是一個純量,
經過輸出層裡的acitvation function 處理完的數字,就會是model 認為是否為1的機率,
再透過decistion boundary 來做最終決策。
像這種不斷把係數由左往右傳遞的手法,由於有向前傳遞的感覺,
所以又被稱為「前傳遞」 forward propagation,有前傳遞就有倒傳遞 backward propagation,
倒傳遞的目地在於更新參數,讓model 在訓練過程中得以不斷修正,
這將會是下一個星期的介紹內容。




 留言列表
留言列表

